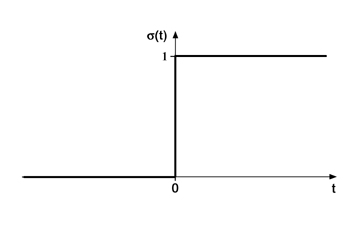
- Sprung-Funktion
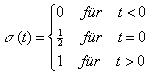
|
Abbildung 3.1: [Wichert, 1991] |
In diesem Kapitel wird die Simulation aufbauend auf den mathematischen Modellen der einzelnen Endgeräte entwickelt. Dazu werden die möglichen Haushaltsverbraucher in geeignete Klassen gegliedert. Die mathematischen Modelle beschreiben zuerst Ein- und Ausschaltleistungssprünge. Danach werden für das transiente Lastverhalten der Verbraucher zwischen den Leistungssprüngen geeignete Näherungen entwickelt. Die charakteristischen Lastgänge der Geräteklassen werden aus einfachen Grundfunktionen aufgebaut, welche hier zuerst vorgestellt werden. Abschließend erfolgt eine Beschreibung von geeigneten Gütekriterien für die Bewertung der Simulation.
Die mathematischen Modelle der einzelnen Endgeräte mittels ihrer Ein- und Ausschaltleistungssprünge und dem transienten Verhalten zwischen diesen, lassen sich mit Hilfe der Addition und Multiplikation von einfachen Grundfunktionen beschreiben. Einige dieser elementaren Funktionen werden hier vorgestellt.
|
|||||
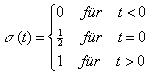
|
Gl.: 3.1 |
|
|||
|
|||||
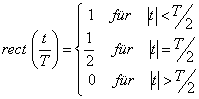
|
Gl.: 3.2
|
|
|||
Mit den zuvor genannten Funktionen lassen sich die Leistungssprünge der Verbraucher modellieren. Dabei ist das transiente Verhalten zwischen diesen Ein- und Ausschaltsprüngen nicht berücksichtigt. Wenn die Leistungsaufnahme nach einem Schaltvorgang nicht konstant ist, gibt es verschiedene Möglichkeiten, sie zu beschreiben. Hier werden erst einmal einige charakteristische Funktionen vorgestellt, die im Weitern verwendet werden:
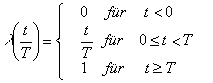
|
Gl.: 3.3
|
|
||||
|
||||||
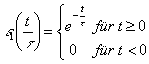
|
Gl.: 3.4
|
|
||||
|
||||||
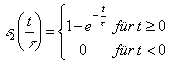
|
Gl.: 3.5
|
|
||||
|
||||||
|
Gl.: 3.6 |
|
||||
|
||||||
|
Standardabweichung :
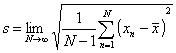 |
Gl.: 3.7 |
|
||||
|
Normalverteilung :
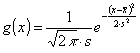 |
Gl.: 3.8 |
|||||
|
||||||
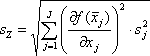 |
Gl.: 3.9 |
| mit: |
sZ = Standardabweichung der berechneten Größe Z,
J = Anzahl der Größen, die in der Berechnung mit einer Streuung behaftet sind,
sj = Standardabweichung der j-ten Größe.
|
Bei der Geräteerkennung mit einem NALM System können die Endgeräte nach unterschiedlichen Kriterien gegliedert werden. Dazu gehören unter anderen der Verwendungszweck, Verwendungsort, Anteil am Gesamtenergiebedarf, Verbrauchscharakteristik und die Steuerung der Geräte. Für diese Arbeit, in der die Endgeräte mit Hilfe ihrer Ein- und Ausschaltleistungssprünge, sowie dem transienten Verhalten zwischen diesen nachgebildet werden sollen, ist nur die Verbrauchscharakteristik der einzelnen Geräte von Bedeutung. Sie wird in vier Geräteklassen gegliedert [Hoberg, 2001]:
Verbrauchscharakteristiken:
Die Klasse der permanenten Verbraucher umfasst alle Geräte, die - sobald sie eingeschaltet sind - dem Netz eine konstante Leistung entnehmen. Dabei ist zu beachten, dass diese Geräte nach der Definition permanent eingeschaltet sind. D. h., sie werden nur selten ein- bzw. ausgeschaltet. Beispiele für diese Verbraucherklasse sind Heizungssteuerungen, Telefonanlagen, Uhren mit Netzbetrieb usw.
Bei den Ein-Aus Verbrauchern handelt es sich um Geräte, die zwei Betriebszustände besitzen. Diese Verbraucher können vom Bediener oder zufällig von einer Steuerung (z. B.: Bewegungsmelder) für eine bestimmte Zeit eingeschaltet werden oder es handelt sich um periodisch schaltende Verbraucher. Die für eine bestimmte Zeit eingeschalteten Geräte wechseln zum Einschaltzeitpunkt vom Aus- in den Ein-Zustand mit den entsprechenden Leistungsaufnahmen. Als Beispiele seien hier genannt: Beleuchtung, Toaster, Wasserkocher, Computer o. ä. Die periodisch schaltenden Verbraucher nehmen, sobald sie eingeschaltet sind, zyklisch ihre Betriebszustände ein. D. h., sie wechseln zum Einschaltzeitpunkt vom Aus- in den Ein-Zustand, nach Ablauf der Dauer des Ein-Zustands in den Stand-By-Zustand und nach dessen Dauer wieder in den Ein-Zustand. Dieses Verhalten wiederholt sich in periodischen Abständen so lange, bis das Gerät ausgeschaltet wird und wieder die Ausschaltleistung aufnimmt. Die Beispiele hierfür sind: Kühlschrank, Gefriertruhe und Klimageräte. Bei diesen periodischen Verbrauchern werden im Folgenden noch Abweichungen für die ersten 3 Ein- bzw. Stand-By-Perioden vorgesehen, da z. B. bei einem Heizlüfter eine Verlängerung der Ein-Zustände zu Beginn auftreten kann. Er heizt nach dem Anlegen der Netzspannung erst einmal so lange die Raumluft auf, bis diese eine bestimmte Temperatur überschritten hat. Erst nach ein paar Schaltperioden kann von einem periodischen Ablauf, abhängig von dem Temperaturverlust pro Zeiteinheit ausgegangen werden.
Die Geräte mit einer Finite-State Charakteristik besitzen mehr als zwei Betriebszustände. Dabei durchlaufen sie diese Zustände sequenziell. D. h., nach dem Einschalten wechseln sie vom Aus-Zustand zum ersten Betriebszustand. Nach der Dauer dieses Zustands wechseln sie in den nächsten und so weiter, bis das Ende des letzten Zustands erreicht ist. Danach nehmen sie eine Stand-By-Leistung auf, bis das Gerät ausgeschaltet wird. Dabei ist es auch möglich, dass der Verbraucher nach einer bestimmten Ausschaltdauer wieder eingeschaltet wird, also der Verlauf periodisch fortgesetzt wird. Der Ablauf dieser Zustände muss nicht immer gleich sein, sondern ist häufig abhängig von dem durch den Benutzer gewählten Programm. Waschmaschine und Geschirrspüler sind Beispiele für diese Klasse.
Als letzte Verbrauchscharakteristik sei die der kontinuierlich variablen Verbraucher genannt. Es handelt sich dabei um Geräte, die dem Netz eine im Voraus nicht genau bekannte Leistung entnehmen. Die Leistungsaufnahme dieser Geräte ist abhängig von unterschiedlichsten Faktoren, die sich zufällig ändern. Dabei kann diese Änderung automatisch hervorgerufen oder vom Benutzer des Elektrogerätes eingestellt werden. Beispiele für diese Verbraucherklasse und die Änderung der Leistungsaufnahme sind die Amplitude und Frequenz des Musiksignals eines Verstärkers oder die Dimmerposition einer Beleuchtungsregelung.
Wie bereits beschrieben, werden für die mathematischen Modelle der Verbraucherklassen als Erstes die Leistungssprünge betrachtet. Dabei ergeben sich zunächst die Sprünge im Lastgang, die entstehen, wenn das Elektrogerät mit dem Netz verbunden oder vom Netz getrennt wird. D. h., für die Geräte aller Verbraucherklassen besteht die Möglichkeit sie ein- bzw. auszuschalten. Nach dem Einschalten verhalten sich die Verbraucher der einzelnen Klassen unterschiedlich. Die Schaltmöglichkeiten aller Endgeräte werden in die folgenden vier Fälle gegliedert. Eine Möglichkeit diese vier Fälle mathematisch zu beschreiben, besteht darin, sie mit der Sprung- oder der Rechteckfunktion aus Gl. 3.1 und 3.2 (Seite 9) zu modellieren.
|
|
|
|
|
|
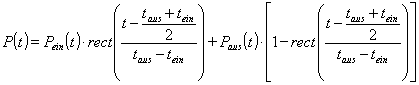 |
|
| mit: |
P(t): Funktion der Leistung des Verbrauchers,
Pein(t):
Funktion der im Ein-Zustand aufgenommenen Leistung,
Paus(t):
Funktion der im Aus-Zustand aufgenommenen Leistung,
|
Wenn ein Verbraucher im betrachteten Zeitraum mehrfach ein- und ausgeschaltet wird, muss der 4. Fall in der Simulation für jede Schaltzeit aufgestellt und diese einzelnen Rechteckfunktionen zur resultierenden Gesamtleistungsfunktion addiert werden.
Elektrogeräte weisen im Betrieb neben den zuvor beschriebenen auch Sprünge von einem zum nächsten Leistungsniveau auf. Diese sind abhängig von der Verbrauchscharakteristik aus Kapitel 3.2, also von der Verbraucherklasse. Wie im vorherigen Abschnitt werden diese Sprünge mit der Addition, Multiplikation sowie der periodischen Fortführung der beiden Grundfunktionen Sprung- und Rechteckfunktion aus Gl. 3.1 und Gl. 3.2 (Seite 9) modelliert.
Die Gruppe der permanenten Verbraucher entnimmt dem Netz eine konstante Leistung. D. h., ein Verbraucher dieser Klasse besitzt neben den generellen Ein- und Ausschaltleistungssprüngen aller Verbraucherklassen keine weitere sprunghafte Leistungsänderung. Mit Hilfe dieser Klasse kann auch ein Ein-Aus Verbraucher, der nur zu einem bestimmten Zeitpunkt geschaltet wird simuliert werden. Dabei ist zu beachten, dass die Leistung im Aus-Zustand nicht gleich Null sein muss.
Die Geräteklasse der Ein-Aus Verbraucher umfasst zwei grundlegende Schaltmöglichkeiten. Das Elektrogerät kann zu einem bestimmten Zeitpunkt ein- bzw. ausgeschaltet werden. Diese Möglichkeit kann mit Hilfe eines permanenten Verbrauchers, der mit den Schalteigenschaften aus Kapitel 3.3.1 verknüpft ist, dargestellt werden. Die zweite Schaltmöglichkeit ist der periodisch schaltende Ein-Aus Verbraucher, der in der Simulation mit dieser Klasse dargestellt wird. Die zwei Betriebszustände werden dann mit der periodischen Fortsetzung der Rechteckfunktion beschrieben. Diese periodische Fortsetzung muss keine feste Periodendauer besitzen, da sie von äußeren Einflüssen abhängig sein kann. Ein Beispiel hierfür ist die Kühlphase einer Gefriertruhe, die von der Außentemperatur, dem Beladungszustand und dem Temperaturverlust beim Öffnen in ihrer Dauer verändert wird. Diese nicht berechenbaren Einflüsse werden in der Simulation mit Hilfe der gaußschen Normalverteilung berücksichtigt. Dabei wird die Dauer eines Zustands als normalverteilt um den Mittelwert mit einer Streuung (Gl. 3.7 / Seite 11) angenommen.
|
|
| mit: |
tein = Einschaltzeit,
Pein(t) = Leistung im Ein-Zustand,
PStBy(t) = Leistung im Stand-By-Zustand,
|
Um die in Kapitel 3.2 beschriebenen Abweichungen der ersten drei Ein- bzw. Stand-By- Perioden zu berücksichtigen, werden in der Simulation Faktoren definiert. Die Dauer der ersten Zustände wird dann im Programmablauf mit dem entsprechenden Faktor multipliziert. Bei periodisch schaltenden Elektrogeräten ist der Energieverbrauch pro Jahr bzw. Tag eine signifikante Eigenschaft und wird häufig in den Datenblättern mit einer Standardabweichung angegeben. Um die elektrische Arbeit zu berechnen, wird das Integral der zeitkontinuierlichen Leistung über eine bestimmte Dauer berechnet. In einem zeitdiskreten System wird hingegen die Summe der einzelnen Leistungswerte mit der Abtastzeit multipliziert. Wenn für diese zeitdiskrete Folge der Leistung eine prozentuale Streuung angenommen wird, ergibt sich auch für die Standardabweichung der Leistung ein zeitabhängiger Verlauf. Da die Arbeit pro Tag auch aus der mittleren Leistung und Dauer der Zustände berechnet werden kann, ist es möglich, die prozentuale Streuung der Ein- und Ausschaltdauer aus der Standardabweichung der Arbeit, den Mittelwerten der Leistungen und ihrer Streuungen in % mit Hilfe der Fehlerfortpflanzung aus Gl. 3.9 (Seite 12) näherungsweise zu berechnen.
|
|
|||
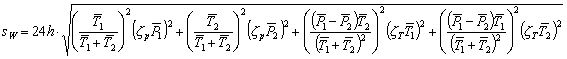 |
|
||
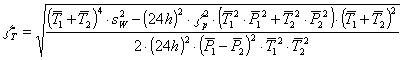 |
|
||
| mit: |
+
zT
= Streuung der Periodendauer in %,
zP
= Streuung der Leistung in %,
|
Wenn das Gerät nicht periodisch schaltet, aber die Dauer der Betriebszustände trotzdem mit einer Standardabweichung behaftet sein soll, ist es notwendig, diese mit Hilfe der mittleren aufgenommenen elektrischen Arbeit über eine Ein- und Ausschaltperiode mit deren Streuung zu berechnen.
|
|
|||
|
|
|||
| mit: |
zT
= Streuung der Periodendauer in %,
zP
= Streuung der Leistung in %,
|
Die einzelnen Betriebszustände der Finite-State Verbraucher sind durch die Addition von Rechteckfunktionen zu modellieren. Dabei werden diese hintereinander gereiht, d. h., das Ende eines Impulses ist auch gleichzeitig der Start des nächsten. Auch hier wird im Modell angenommen, dass die Dauer des einzelnen Zustands nicht immer gleich ist. Sie wird - wie beim Ein-Aus Verbraucher - normalverteilt um einen Mittelwert berechnet.
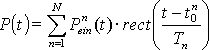 |
|
| mit: |
tein = Einschaltzeit,
N = Anzahl der Zustände,
|
Der Finite-State Verbraucher kann auch ein periodisch schaltendes Elektrogerät darstellen. Dabei wird der Funktionsverlauf nach einer Stand-By Zeit wiederholt. Die Periodendauer ergibt sich aus den einzelnen Zustandsabfolgen und der Stand-By Zeit.
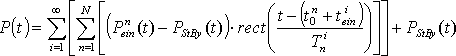 |
|
| mit: |
tein = Einschaltzeit,
N = Anzahl der Zustände,
PStBy (t)
= Dauer des n-ten Zustands,
|
Auch bei den periodisch fortgesetzten Finite-State Verbrauchern ist der Energieverbrauch pro Tag eine wichtige Größe. Genau wie bei den Ein-Aus Verbrauchern soll hier die Standardabweichung der einzelnen Betriebszustände aus den Streuungen der Leistung und der aufgenommenen elektrischen Arbeit pro Tag Gl. 3.19, oder pro Periode Gl. 3.20 errechnet werden.
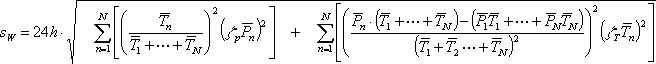 |
|||
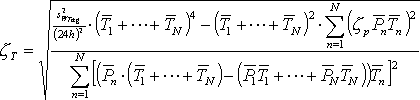 |
|||
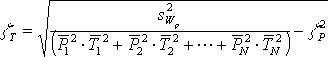 |
|||
| mit: |
zT
= Streuung der Periodendauer in %,
zP = Streuung der Leistung in %,
|
||||||||
Die Klasse der kontinuierlich variablen Verbraucher ist mit einem NALM System kaum zu erkennen, weil sie keine fest definierten Leistungssprünge besitzt. Bei der Simulation kann sie mit der Klasse der permanenten Verbraucher mit einem zufälligen Lastverlauf gleichgesetzt werden. Dieser zufällige Verlauf der Leistungsaufnahme wird im Folgenden beschrieben.
Die Leistungssprünge der einzelnen Endgeräte sind mit der Sprung- und Rechteckfunktion mathematisch definiert worden. Jetzt muss das Lastverhalten zwischen diesen Sprüngen betrachtet werden. Als erste Möglichkeit sei hier die konstante Leistungsaufnahme genannt. Dabei entnimmt der Verbraucher dem Netz nach dem Wechsel des Betriebszustands eine genau bekannte, für den Zustand immer gleiche Leistung.
| P(t) = P |
| mit: |
P(t) = Leistungsaufnahme zum Zeitpunkt t,
P = konstanter Leistungswert.
|
|
Da der Energieverbrauch eines elektrischen Verbrauchers zu einem definierten Betriebszustand von den unterschiedlichsten Bedingungen abhängig ist, nehmen die Meisten keine über die Dauer des Zustands konstante Leistung auf. Eingangsgrößen, die das Lastverhalten beeinflussen, können sich zufällig ändern. Als Beispiel sei hier die Spannung des Versorgungsnetzes genannt, die nach DIN IEC 38 eine erlaubte Toleranz von + 6% und -10% um den Mittelwert von 230 Volt besitzt. Diese Schwankung der Spannung ist von stochastischer Natur. Um eine solche Änderung der Eingangsgrößen in der Simulation berücksichtigen zu können, wird im Weiteren die aufgenommene Leistung mit einer prozentualen Streuung um den Leistungswert nach der gaußschen Normalverteilung (Gl. 3.8 / Seite 11) angenommen. Diese zufälligen Schwankungen der Last können auch gerätespezifische Eigenschaften sein, wie zum Beispiel bei den kontinuierlich variablen Verbrauchern, wo die Leistungsaufnahme - wie in Kapitel 3.2 beschrieben - von der Amplitude und der Frequenz eines Musiksignal am Eingang eines Verstärkers abhängig sein kann. Auch diese verbraucherabhängigen Größen werden in der Simulation mit Hilfe der Gaußverteilung berücksichtigt, wobei die Streuung entsprechend groß gewählt wird. Da die Normalverteilung eine statistische Berechnung der Abweichung einzelner Messwerte von dem arithmetischen Mittelwert ist, kann sie nicht auf zeitkontinuierliche Funktionen angewendet werden. Die zu entwickelnde Simulation bildet den Lastverlauf nach, wie er bei einem NALM System aufgenommen wird. Dabei handelt es sich - wie in Kapitel 2.3 beschrieben - um quantisierte Leistungswerte zu diskreten Zeit-punkten, die mit Hilfe statistischer Methoden betrachtet werden können. Auf die Quantisierung und Zeitdiskretisierung des Simulationsmodells wird in Kapitel 3.4 näher eingegangen, so dass hier zufällige Laständerungen mit der gaußschen Normalverteilung angenommen werden können.
|
P(t) =
|
| mit: |
P(t) = Leistungsaufnahme zum Zeitpunkt t,
DP(t) = Leistungsdifferenz zum Zeitpunkt t
nach gaußscher Normalverteilung.
|
|
Neben den zufälligen Leistungswerten gibt es Lastverläufe, die einer gerätespezifischen Funktion folgen. Diese Verläufe können unterschiedliche Formen besitzen. Die unterschiedlichsten Möglichkeiten dieser Lastverläufe sollen mit dem Simulationsmodell nachgebildet werden können. Häufig kommt es nach dem Umschalten in einen neuen Betriebszustand zu einer kurzfristigen Leistungserhöhung (Peak) oder zu einem verzögerten Anstieg der Leistung auf den Endwert. Diese Starteigenschaften sollen in der Simulation mit einfachen Funktionen nachgebildet werden. Die einfachste Form eines Startvorgangs ist die Erhöhung bzw. Verringerung der Leistung für einen festen Zeitraum auf eine konstante Startleistung. Diese Nachbildung kann verwendet werden, wenn der reale Verlauf wegen der Glättung aus dem Messverfahren bei einem NALM System nicht zu erkennen ist. Er kann mit Hilfe des Modells eines Finite-State Verbrauchers mit zwei Betriebszuständen - jeweils konstante Leistungsaufnahme - mathematisch beschrieben werden. Eine weitere mögliche Funktion der Leistung ist der lineare Anstieg bzw. Abfall von einem Start- auf einen Endwert. Dieser lineare Verlauf kann mit einer kurzen Steigungsdauer die Startcharakteristik eines Verbrauchers simulieren oder mit einer Steigung über die gesamte Periode des Betriebszustands einen konstanten Lastabfall auf 95% der Startleistung einiger Kühlgeräte [Hoberg, 2001] darstellen.
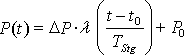 |
| mit: |
P(t) = Leistungsaufnahme zum Zeitpunkt t,
t0 = Startzeit,
TStg = Steigungsdauer,
P0 = Startleistung,
PEnd = Endleistung,
DP = PEnd
- P0 = Leistungsdifferenz.
|
||
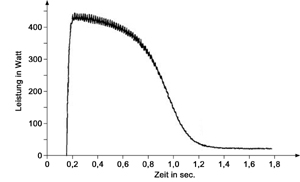
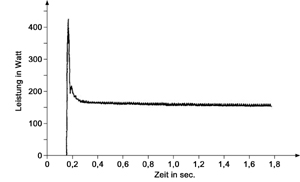
Die Abbildungen 3.8 und 3.9 (nächste Seite) zeigen zwei Beispiele realer Lastverläufe. Es ist zu erkennen, dass diese Startvorgänge in einer sehr kurzen Zeit ablaufen. Der Induktionsmotor in Abbildung 3.8 hat nach ca. 1,0 Sekunden seinen konstanten Endwert erreicht. Bei dem Lichtband aus Leuchtstofflampen in Abbildung 3.9 dauert dieser Vorgang nur ca. 0,1 Sekunden. Wenn nun noch beachtet wird, dass diese Kennlinien durch das Messverfahren bei einem NALM System stark geglättet werden (Kapitel 2.4 bzw. Abbildung 2.3 / Seite 8), sind diese Verläufe mit Hilfe der e-Funktionen aus Gl. 3.4 und 3.6 (Seite 10 + 11) näherungsweise gut zu beschreiben. Da die Exponentialfunktion, mit der Euler'schen Zahl e als Basis, häufig Ausgangsgrößen in der Elektrotechnik darstellt, werden die in Kapitel 3.1 gezeigten Variationen der e-Funktion in die Simulation zur möglichen Nachbildung des Lastverhaltens von Elektrogeräten verwendet.
Die Funktion aus Gl. 3.6 (Seite 11) besitzt nur über die Steigungszeit Gültigkeit. Sie muss daher noch mit der Rechteckfunktion, die die Steigungszeit als Dauer enthält, multipliziert werden. Auch beginnt sie nicht genau bei ihrem Startleistungswert, sondern bei 99,33 % dieses Wertes. Wenn die zuvor genannten Bedingungen berücksichtigt werden, ist diese Funktion geeignet, den Startvorgang des Induktionsmotors aus Abbildung 3.8, näherungsweise zu beschreiben.
 |
 |
||||||
|
|
|
|
|||
| mit: |
P(t) = Leistungsaufnahme zum Zeitpunkt t,
t0 = Startzeit,
TStg = Steigungsdauer,
P0 = Startleistung,
PEnd = Endleistung,
DP = PEnd
- P0 = Leistungsdifferenz.
|
Die vorgestellten Funktionen sollen ermöglichen, alle Schaltzustände der elektrischen Verbraucher in privaten Haushalten in einer akzeptablen Näherung modellieren zu können. Dabei werden die Schaltzustände mit ihrem transienten Verhalten in Abhängigkeit der Form, der Startzeit, der Schaltdauer, der Start-, der Endleistung und der Steigungszeit beschrieben.
Wie bereits im Kapitel 2.3 erläutert, kann zur Ermittlung der Leistungsaufnahme der Impulsausgang eines Zählers verwendet werden. In diesem Fall handelt es sich bei dem resultierenden Lastgang um quantisierte Leistungswerte zu diskreten Zeitpunkten. Dabei ist die Quantisierung der Leistungswerte abhängig von der Impulskonstante des Zählers. Sie wird in der Simulation vorgenommen, nachdem der Gesamtlastgang aus der Summe des Energieverbrauchs aller Elektrogeräte gebildet worden ist. Die Zeitdiskretisierung wird mit einem festen Abtastintervall erreicht. Auch in der Simulation des Lastgangs sollen Leistungswerte für bestimmte Zeitintervalle berechnet werden. Diese Intervalle sind durch den Anwender variabel vorzugeben. Um die Zeitdiskretisierung zu erreichen, muss der Mittelwert der Leistung über die Periodendauer des Abtastintervalls berechnet werden. Dazu wird das bestimmte Integral der Leistungsfunktion über die Abtastzeit berechnet und durch die Abtastperiodendauer geteilt. Aus diesen einzelnen Leistungswerten Pk wird eine zeitdiskrete Folge ( Pk ) gebildet.
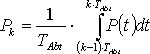 |
|
| mit: |
( Pk ) = zeitdiskrete Folge der Leistungsmittelwerte,
Pk = k-ter Leistungswert der Folge,
TAbt = Periodendauer des Abtastintervalls,
P(t) = zeitkontinuierliche Funktion der Leistung.
|
Bei einem, über das gesamte Abtastintervall stetigen Leistungsverlauf, wird das unbestimmte Integral dieser Funktion aufgestellt und die Grenzen zur Berechnung des bestimmten Integrals eingesetzt. Dieses stellt die mittlere geleistete Arbeit von der unteren bis zur oberen Grenze dar und damit kann, dividiert durch die Integrationszeit, die mittlere aufgenommene Leistung bestimmt werden. Wenn die Funktion innerhalb des Abtastintervalls nicht stetig verläuft, muss das Integral in einzelne stetige Abschnitte der Funktion unterteilt werden. Zuerst muss der Zeitraum von der unteren Grenze bis zur ersten Unstetigkeitsstelle integriert werden. Der nächste zu integrierende Abschnitt läuft dann bis zur nächsten Unstetigkeit oder bis zur oberen Grenze des bestimmten Integrals.
Die Funktionen mit einem konstanten Leistungsverlauf nach der Gl. 3.21 und 3.22 (Seite 18) und die ersten beiden Verläufe mit der e-Funktion nach den Gl. 3.24 und 3.25 (Seite 20) sind für t ![]() 0 stetige Funktionen. Die lineare Funktion aus Gl. 3.23 (Seite 19) und der letzte Lastverlauf mit der e-Funktion nach Gl. 3.26 (Seite 20) sind dagegen unstetig. Eine weitere Unstetigkeitstelle ergibt sich, wenn der Verbraucher während des Abtastintervalls umgeschaltet wird, wodurch sich der Funktionsverlauf der Leistung ändert. Die folgenden Formeln zeigen die Berechnung der mittleren Arbeit der verschiedenen Verlaufsformen.
0 stetige Funktionen. Die lineare Funktion aus Gl. 3.23 (Seite 19) und der letzte Lastverlauf mit der e-Funktion nach Gl. 3.26 (Seite 20) sind dagegen unstetig. Eine weitere Unstetigkeitstelle ergibt sich, wenn der Verbraucher während des Abtastintervalls umgeschaltet wird, wodurch sich der Funktionsverlauf der Leistung ändert. Die folgenden Formeln zeigen die Berechnung der mittleren Arbeit der verschiedenen Verlaufsformen.
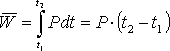 |
|
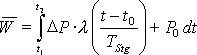 |
|
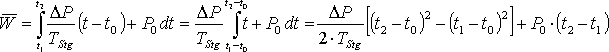
|
|||
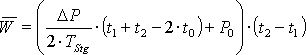
|
|||
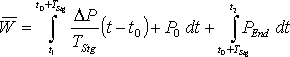
|
|||
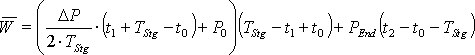
|
|
||
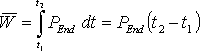
|
|
||
1) |
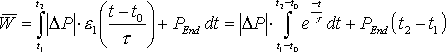 |
|||
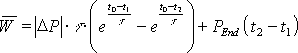 |
|
|||
2) |
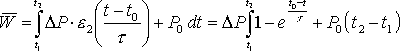 |
|||
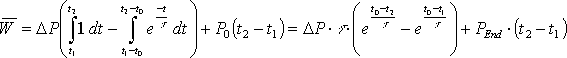 |
|
|||
3) |
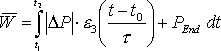 |
|
||
|
|
||||
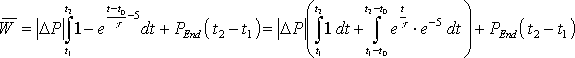 |
||||
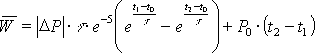 |
|
|||
|
|
||||
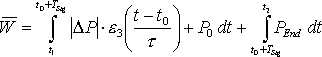 |
||||
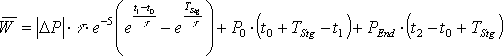 |
|
|||
|
|
||||
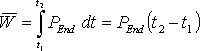 |
|
|||
|
t1 = Start- und t2
= Stoppzeitpunkt der Integration,
t0 = Zeitverschiebung derFunktion,
TStg = Steigungsdauer der Funktion,
P0 = Startleistung der Funktion,
PEndEndleistung der Funktion,
DP = PEnd
- P0 = Leistungsdifferenz.
|
Wenn die einzelnen bestimmten Integrale innerhalb der Abtastperiode berechnet und addiert worden sind, muss die Summe durch die Abtastzeit dividiert werden. Damit ergibt sich der, über die Abtastzeit gemittelte, zeitdiskrete Leistungswert.
Die Quantisierung der Leistungswerte des Gesamtlastgangs erfolgt mit der Impulskonstante des Energiezählers. Diese wird in Impulse pro kWh angegeben. Für die Quantisierung wird der Energiewert pro Impuls benötigt. Jeder einzelne zeitdiskrete Leistungswert wird mit der Abtastzeit multipliziert und das Produkt durch den Energiewert pro Impuls dividiert. Der Ganzzahl-Anteil des Quotienten multipliziert mit dem Energiewert pro Impuls ergibt den quantisierten Leistungswert. Der Nachkomma-Anteil muss mit dem Energiewert pro Impuls multipliziert und beim nächsten Leistungswert berücksichtigt werden. D. h., dass er zum Produkt aus dem Leistungswert und der Abtastzeit des nächsten zeitdiskreten Wertes hinzu addiert wird.
 |
|
||
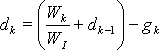 |
|
||
|
|
|||
| mit: |
Pk = k-ter Leistungswert der Folge,
TAbt = Periodendauer des Abtastintervalls,
Wk = Pk
+
KI = Impulskonstante des Zählers,
|
Jetzt wird an Hand zweier Beispiele gezeigt, wie ein Verbraucher mit den zuvor beschriebenen mathematischen Funktionen modelliert werden kann. Dabei wird im Einzelnen darauf eingegangen, in welcher Reihenfolge und mit welchen Bedingungen die Eigenschaften eines Elektrogerätes in das Gesamtmodell integriert werden.
Um den in diesem Beispiel gegebenen kontinuierlich variablen Verbraucher nachbilden zu können, werden die nachfolgend angegebenen Daten benötigt. Dabei wird die Startzeit des Betrachtungszeitraumes nicht absolut gewählt. D. h., dass sie gleich Null gesetzt wird und die anderen Zeiten relativ zur Startzeit angegeben werden.
Mit den gegebenen Werten wird als erstes die Rechteckfunktion für die Einschaltzeit gebildet. Zur gesamten Funktion wird dann die Aus-Leistung aufaddiert und daher die Rechteckfunktion mit der Differenz aus Ein- und Aus-Leistung multipliziert. Diesen ersten Schritt zeigt die Formel unter Gl. 3.34.
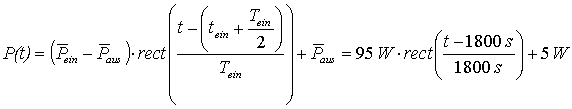
|
|
Die resultierende Leistung in Abhängigkeit der Zeit stellt den zeitkontinuierlichen Verlauf dar. Im nächsten Schritt wird diese Funktion zeitdiskretisiert. Zu diesen Werten addieren sich die zufälligen, mit Hilfe der gaußschen Normalverteilung bestimmten Leistungsabweichungen DPk hinzu. Dabei ist zu beachten, dass die Streuung als Grundlage für die zufällig gewählten Abweichungen während der Einschaltzeit größer ist als im ausgeschalteten Zustand.
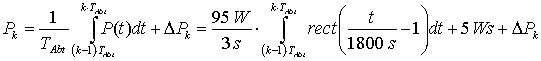 |
|
| mit: |
|
Damit liegt die zu zeichnende zeitdiskrete Folge des Lastgangs für den simulierten Verbraucher vor.
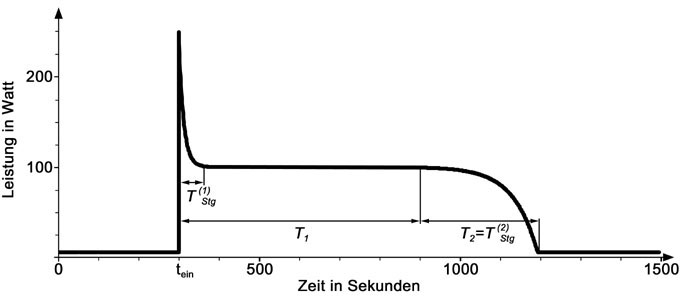
Der gegebene Finite-State Verbraucher soll über den gesamten betrachteten Zeitraum von einem Tag mit dem elektrischen Versorgungsnetz verbunden sein. Er besitzt drei Betriebszustände, wobei einer dem Stand-By-Betrieb entspricht. Diese Zustände werden nacheinander durchlaufen und periodisch wiederholt. Der erste Bereich der Lastkurve soll nach der e-Funktion aus Gl. 3.4 (Seite 10) verlaufen, der zweite nach der e-Funktion aus Gl. 3.6 (Seite 11). Im Stand-By-Zustand entspricht die aufgenommene Leistung einem konstanten Wert. Die einzelnen Daten sind wie folgt gegeben. Zum besseren Verständnis ist ein Ausschnitt aus der idealen zeitkontinuierlichen Lastganglinie über jeweils eine Periodendauer des 1. und 2. Zustands in Abbildung 3.10 dargestellt. In dieser Darstellung ist die Streuung der zeitdiskreten Leistungswerte nicht berücksichtigt.
| Streuung der vom Verbraucher pro Tag aufgenommenen Arbeit: | = 6 Wh ; |
|
mittlere Dauer: |
= 250 W ; | = 100 W ; |
| Steigungsdauer der e-Funktion: 5 | = 60 s. |
|
mittlere Dauer:
|
= 100 W ; | = 5 W ; |
| Steigungsdauer der e-Funktion: 5 | . |
 |
||
|
Da der Verbraucher dauerhaft mit dem Netz verbunden ist, sind keine Leistungssprünge beim Ein- bzw. Ausschalten zu beachten. Sein Zustand zu Beginn des Betrachtungszeitraums wird zufällig gewählt, daher wird in der Formel eine Zeitverschiebung = t0 verwendet.
Im ersten Schritt müssen die Rechteckfunktionen der ersten beiden Zustände gebildet werden. Zur Summe dieser beiden wird die Stand-By-Leistung addiert:
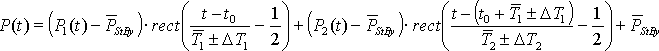 |
|||
|
|
|||
In diese Gleichung werden nun die beiden zeitabhängigen Funktionen der Leistung eingefügt:
|
|
|||
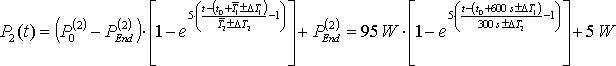
|
|||
|
|
|||
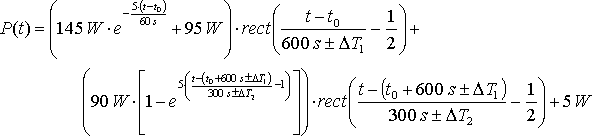 |
|||
|
|
|||
Jetzt wird die prozentuale Streuung für die Periodendauer der einzelnen Zustände mit Hilfe der Gl. 3.20 (Seite 17) berechnet. Dazu ist es notwendig die mittlere Leistungsaufnahme der einzelnen Zustände zu bestimmen:
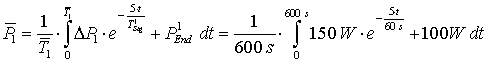
|
|||
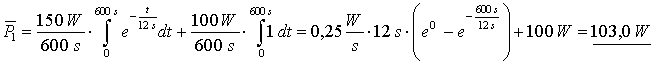
|
|||
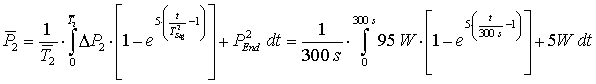
|
|||
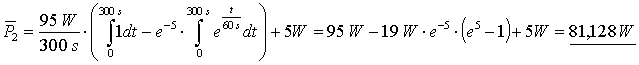
|
|
||
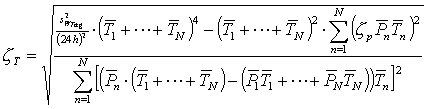 |
|
||
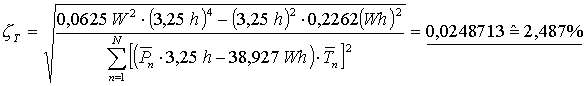
|
|||
Mit dieser prozentualen Streuung können nun die Abweichungen der Periodendauer für die einzelnen Zustände zufällig gewählt werden und die Funktion der Leistung aus Gl. 3.37 (vorherige Seite) wird periodisch wiederholt. Dazu muss die Zeitverschiebung jedes k-ten 1. Zustands ![]() bestimmt werden:
bestimmt werden:
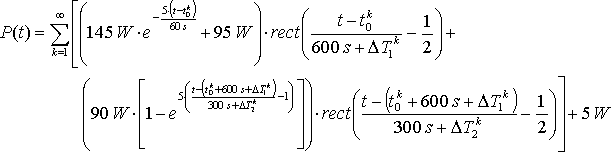
|
||
|
|
| mit: | |||
|
|
|||
Die Summe für die Wiederholung der Zustände läuft in der Formel bis ![]() , weil die zufälligen Abweichungen der Periodendauern erst beim Berechnen des Lastgangs gesetzt werden. Die Summe wird abgebrochen, wenn das Ende des Betrachtungszeitraums erreicht ist.
Auch die Zeitdiskretisierung kann erst vorgenommen werden, wenn der Lastgang mit der Formel aus Gl. 3.39 explizit mit allen zufällig zu wählenden Größen berechnet wird
, weil die zufälligen Abweichungen der Periodendauern erst beim Berechnen des Lastgangs gesetzt werden. Die Summe wird abgebrochen, wenn das Ende des Betrachtungszeitraums erreicht ist.
Auch die Zeitdiskretisierung kann erst vorgenommen werden, wenn der Lastgang mit der Formel aus Gl. 3.39 explizit mit allen zufällig zu wählenden Größen berechnet wird
In diesem Abschnitt werden Kriterien beschrieben, mit denen die Simulation qualitativ bewertet werden kann. Sie sollen helfen, die in der Simulation verwendeten einzelnen Modelle der elektrischen Verbraucher zu verifizieren bzw. zu validieren und ggf. anzupassen.
Als erster Anhaltspunkt zur Bewertung des nachgebildeten Lastgangs bietet sich der Vergleich des simulierten mit dem realen Gesamtenergieverbrauch über den betrachteten Zeitraum an. Um die dem Netz entnommene elektrische Arbeit zu berechnen, muss die Summe aller zeitdiskreten Leistungswerte, multipliziert mit der Abtastperiodendauer, gebildet werden.
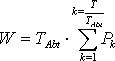
|
|
||
| mit: | W = aufgenommene elektrische Arbeit, |
||
TAbt = Abtastperiodendauer, |
|||
T = Dauer des betrachteten Zeitraums, |
|||
|
Pk = k-ter Leistungswert der zeitdiskreten Folge und
|
Danach kann kontrolliert werden, ob der Betrag der Differenz aus der real aufgenommenen Arbeit und der simulierten in einem gewählten Fehlerbereich liegt:
|
|
| mit: |
Wges = realer Gesamtenergieverbrauch,
|
||
|
Wsim = simulierter Gesamtenergieverbrauch,
|
|||
e = gewählte Fehlerschranke. |
Die Grenzen des Fehlerbereichs können mit einer Abschätzung der Streuung der Gesamtarbeit gewählt werden. Da sich der Energieverbrauch der einzelnen Endgeräte zu gesamten aufgenommenen Arbeit addiert, errechnet sich die Standardabweichung des resultierenden Verbrauchs nach Gl. 3.9 (Seite 12) mit der folgenden Formel. Diese Berechnung gilt nur bei zufälligen Abweichungen:
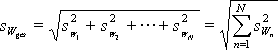
|
|
| mit: |
|
||
|
|
|||
|
|
Die Streuungen der Verbraucher müssen dafür ggf. auf den betrachteten Zeitraum umgerechnet werden. Zusätzlich müssen evtl. Abbruchfehler beachtet werden, die z.B. entstehen können, wenn bei einem periodisch schaltenden Elektrogerät keine ganzzahlige Anzahl von Perioden im resultierenden Lastgang enthalten ist. Dieser Fehler wird umso kleiner, je größer der betrachtete Zeitraum gewählt wird.
Neben dem Gesamtenergieverbrauch kann zur Bewertung der Simulation auch der Verbrauch über einen bestimmten Zeitraum oder der einzelner elektrischen Geräte verglichen werden. Dazu bieten sich Betrachtungen über einen Tag oder ein Jahr an. Weiterhin kann der Energieverbrauch während eines Schaltzustands eines Gerätes und bei den Ein-Aus bzw. Finite-State Verbrauchern zusätzlich während einer Schaltperiode bewertet werden. Der reale Lastgang kann nicht immer genau in den Energieverbrauch der einzelnen Elektrogeräte aufgeteilt werden. Daher ist die Betrachtung der von den Verbrauchern aufgenommenen Leistung evtl. schwierig.
Der Energieverbrauch ist nur eine erste Abschätzung der Güte des simulierten Lastgangs. Damit ist noch keine Aussage über den zu bewertenden Verlauf möglich. Als Beispiel sei hier der Energieverbrauch eines periodisch schaltenden Verbrauchers genannt, der im Aus-Zustand keine und im Ein-Zustand eine konstante Leistung aufnimmt. Dabei ist die aufgenommene Arbeit abhängig von dem Leistungswert und der Dauer des Ein-Zustands. Der Energieverbrauch ist also bei einer kleinen Ein-Leistung über einen langen Zeitraum gleich dem über einer kurzen Zeit auf hohem Leistungsniveau. Daraus ergibt sich die Notwendigkeit die einzelnen Verbraucher hinsichtlich der Zeitpunkte der Leistungssprünge und dem transienten Verhalten zwischen diesen zu untersuchen.
Um die Qualität des Verlaufs der simulierten Lastkennlinie zu bewerten, kann die Summe der Abweichungen des simulierten zum realen Energieverbrauch betrachtet werden. Um diese Summe zu berechnen, wird der reale Lastgang vom simulierten subtrahiert und die Beträge der Integrale über die positiven sowie die negativen Abweichungen addiert. Da es sich bei beiden Lastgängen um zeitdiskrete Folgen handelt, ist die Berechnung dieser Integrale auf die Multiplikation von Zeit- mit Leistungswerten reduziert. Die Summe aus den Beträgen dieser Produkte ergibt die gesamte Abweichung der Lastgänge voneinander.
In den folgenden Berechnungen wird davon ausgegangen, dass die beiden zu vergleichenden Lastgänge und der Vergleichszeitraum zum selben Zeitpunkt starten und enden. Da bei der Simulation die Startzeit frei gewählt werden kann, ist diese Voraussetzung relativ leicht zu erfüllen. Wenn nur ein Ausschnitt aus einem realen Lastgang simuliert werden soll, ist es notwendig, die Startzeit der Simulation auf den Start eines Abtastintervalls zu setzen und den Index dieses ersten zu beachtenden Leistungswertes in den Berechnungen zu berücksichtigen. Das bedeutet, dass der Indexwert in der Berechnung bei den zeitdiskreten Werten der Folge des realen Lastgangs zum Index hinzuaddiert werden muss.
 |
|||
|
|
Die Abweichung zweier Lastgänge mit gleicher Länge der Abtastintervalle
( T1 = T2 ).
|
||
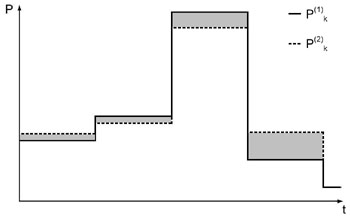
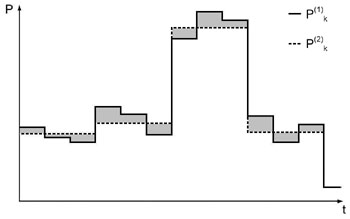
Wenn die Abtastintervalle des realen und simulierten Lastgangs die gleiche Länge besitzen, reicht es, die Beträge der Subtraktion der einzelnen zeitdiskreten Leistungswerte zu addieren und die Summe mit der Abtastdauer zu multiplizieren. Die Beträge berechnen sich mit der positiven Wurzel aus den Quadraten der Subtraktion. Die Abbildung 3.11 zeigt den Ausschnitt zweier Lastgänge mit gleicher Dauer der Abtastperioden (T1 = T2). Die grau dargestellten Flächen zeigen die Abweichungen der Kennlinien voneinander. Die Berechnung des Fehlers erfolgt mit der folgenden Formel:
|
|
|||
| mit: |
E = Fehler der Simulation, d.h.: Gesamtabweichung der Lastgänge voneinander,
|
||
|
img src="images/formel3-041.gif" width="25" height="23" border="0" alt="" align="middle">
= k-ter Wert der Folge des realen Lastgangs,
|
|||
|
|
|||
|
T1 = T2
= TAbt = Dauer der Abtastintervalle,
|
|||
|
k1 = 1 =
Index des 1. Leistungswertes des realen Lastgangs im Betrachtungszeitraum,
|
|||
|
|
|||
|
T = n
|
|||
 |
|||
|
Die Abweichung zweier Lastgänge mit 3T1
= T2 .
|
|||
Wenn die Abtastperiodendauer des einen zu vergleichenden Lastgangs eine ganzzahlige Vielfache der anderen ist und die Startzeit des ersten Intervalls gleich ist, muss innerhalb des größeren Abtastintervalls die Summe der Leistungsdifferenzen des kleineren Intervalls gebildet werden und mit der kleineren Abtastzeit multipliziert werden. Die Abbildung 3.12 zeigt ein Beispiel für diese Konstellation in einem Ausschnitt über einige Abtastperioden. Der Fehler ist wiederum grau eingefärbt.
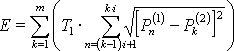
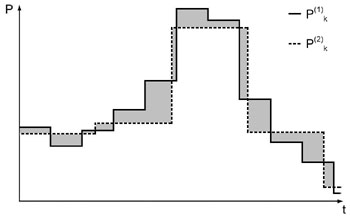
|
|
| mit: |
E = Fehler der Simulation, d.h.: Gesamtabweichung der Lastgänge voneinander,
|
||
|
|
|||
|
|
|||
|
T1 = Dauer der Abtastintervalle des 1. und
T2
= des 2. Lastgangs mit T2 = i
|
|||
|
k1
= 1 = Index des 1. Leistungswertes des realen Lastgangs im Betrachtungszeitraum,
|
|||
|
|
|||
|
T = m
|
 |
|||
|
Die Abweichung zweier Lastgänge mit
|
|||
In den zuvor behandelten Fehlerberechnungen der Simulation werden gleiche Start- und Stoppzeiten der beiden Lastgänge und des Betrachtungszeitraums vorausgesetzt. Weiterhin muss das evtl. größere Abtastintervall ein ganzahliges Vielfaches des kleineren sein. Wie bereits erwähnt, sind diese Vorraussetzungen durch eine geeignete Wahl der Startzeit und der Abtastperiode für die Simulation zu realisieren. Es können aber Fälle vorliegen, bei denen diese Voraussetzungen nicht erfüllt werden. Die Abtastintervalle der beiden Lastgänge können sich dann überschneiden. Die Abbildung 3.13 zeigt ein Beispiel einer solchen Überschneidung, die sich ergibt, wenn die größere Abtastperiode eine nicht ganzzahlige Vielfache der kleineren ist. Die Abweichung der beiden Lastgänge voneinander ist auch hier grau gekennzeichnet. Eine Überschneidung der Abtastperioden kann aber auch aus unterschiedlichen Startzeiten der beiden Lastgänge herrühren. Wenn nun auch noch der Fehler über einen beliebigen Zeitraum berechnet werden soll, ist die mathematische Beschreibung dieser Berechnung kompliziert. Daher soll hier ein Algorithmus vorgestellt werden, mit dem diese Berechnung durchgeführt werden kann.
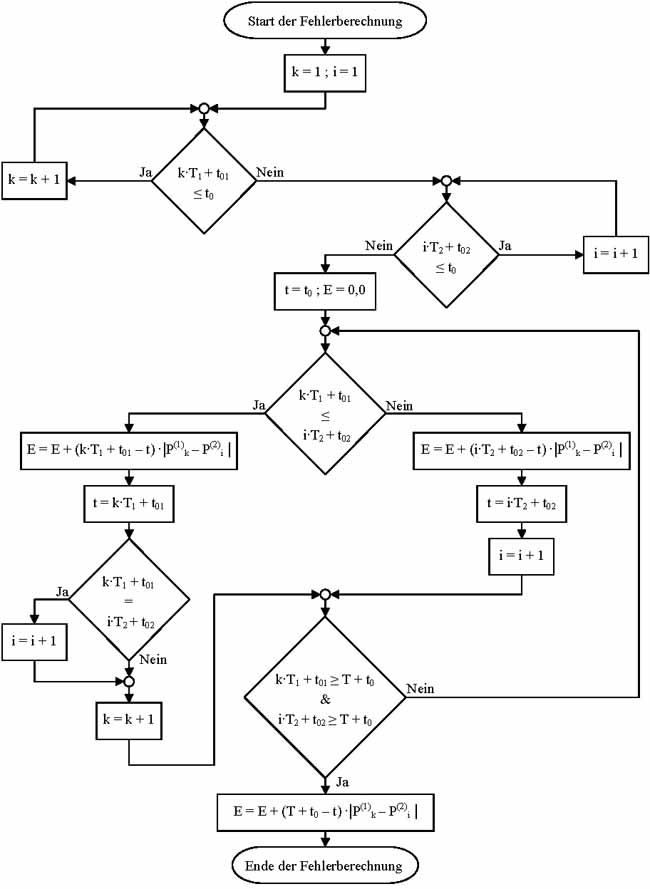
Um den Fehler zweier Lastgänge zu berechnen, muss zuerst der Zeitraum bestimmt werden, über den die Gesamtabweichung bestimmt werden soll. Weil die Berechnung zu absoluten Zeitpunkten erfolgt, müssen auch die Startzeiten der beiden Lastgänge mit ihren Abtastintervallen bekannt sein. Des Weiteren werden zwei Laufvariablen für die zeitdiskreten Leistungswerte der Lastgang-Folgen benötigt. In Abbildung 3.14 ist der Algorithmus dieser Berechnung in Form eines Flussdiagramms zu sehen. Dabei ist es notwendig, zuerst die Indizes zu bestimmen, die die beiden Leistungswerte der Lastgänge zum Startzeitpunkt des Berechnungszeitraums in ihrer Folge besitzen. Danach werden die Abweichungen jeweils bis zum nächsten Zeitpunkt, zu dem sich die Leistung eines der beiden Lastgänge ändert, berechnet und addiert. Dieser Zeitpunkt wird für die nachfolgende Berechnung gespeichert. Begonnen wird dieser Vorgang mit der Startzeit des Berechnungszeitraums. Nach jeder einzeln berechneten Abweichung, wird der Index des Lastgangs, der seinen Leistungswert geändert hat, um 1 erhöht. Wenn die nächsten Abtastintervalle beider Lastgänge nach dem Ende des Berechnungszeitraums starten, wird noch die letzte Abweichung bis dahin bestimmt und aufaddiert. Somit ist der Fehler beider Lastgänge zueinander aus der Summe aller Beträge der Abweichungen berechnet worden. Nachfolgend sind noch die Bezeichnungen aufgelistet, die im Flussdiagramm benutzt werden:
 |
|||
|
Flussdiagramm des Algorithmus zur Berechnung des Fehlers eines simulierten Lastgangs zum realen.
|
|||
Die zuvor beschriebenen Gütekriterien sollen dazu dienen, die Qualität einer Simulation zu bewerten. Welche Fehlerbeschreibung zur Bewertung herangezogen wird, hängt davon ab, worauf bei der Simulation besonderen Wert gelegt wird. Wenn es nicht auf die genaue Wiedergabe des Verlaufs ankommt, reicht es, den Energieverbrauch zu kontrollieren. Dabei ist - wie bereits erwähnt - darauf zu achten, dass zusätzlich die Leistungen in den einzelnen Schaltzuständen und deren Einschaltzeiten kontrolliert werden müssen. Falls der Verlauf möglichst genau dargestellt werden soll, bietet der Fehler der Simulation nach dem Algorithmus aus Abbildung 3.14 (vorherige Seite) eine Bewertungsmöglichkeit. Dieses Gütekriterium berücksichtigt alle Abweichungen vom realen Lastgang.