|
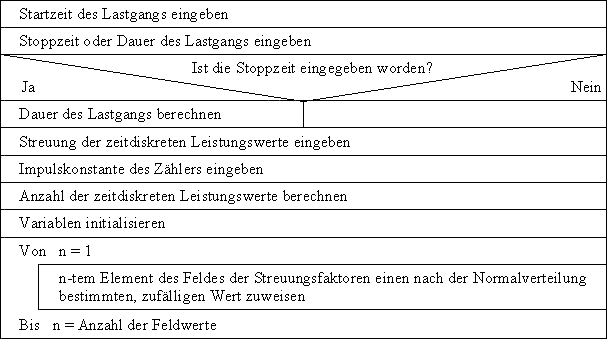
Funktion "Setze Lastgangeinstellungen" des Hauptprogramms
|
Nun wird beschrieben, wie die mathematischen Modelle der einzelnen Verbrauchergruppen mit Hilfe einer objektorientierten Programmiersprache in einen Softwaresimulator implementiert werden können. Dazu werden zuerst die Grundlagen und einige Begriffe der objektorientierten Softwareentwicklung beschrieben.
Die objektorientierte Programmierung hat die rationelle Softwareentwicklung zum Ziel. Zu den Vorteilen dieser Programmierungsform gehören u. a. die dynamische Modellerzeugung, eine schnelle Anpassung an veränderte Randbedingungen, leichtes Ändern bzw. Einfügen neuer Eigenschaften und Methoden und die Wiederverwendung bereits entwickelter Modelle. Dazu werden die Modelle abstrahiert und in Klassen beschrieben. Die Daten der Objekte sind gekapselt. Klassen können ihre Datenstruktur und Methoden vererben und Funktionsabläufe dynamisch gewählt werden. Im Folgenden sind die benutzten Begriffe aufgelistet und definiert.
Abstraktion bedeutet, dass ein Objekt durch seine wesentlichen Eigenschaften beschrieben wird. Dabei kann ein Objekt ein Gegenstand aus der realen Welt, eine Methode oder ein Algorithmus sein. Mit der Abstraktion wird erreicht, diese Objekte im Rechner abbilden (simulieren) zu können. Die Abbildung wird Objekt genannt.
Die Beschreibung eines Objektes heißt Klasse. Sie besteht aus der inneren Datenstruktur und die darauf anwendbaren Funktionen oder Methoden. Zur Datenstruktur gehören die Namen und Formate der einzelnen Parameter. Objekte werden auch als Instanzen einer Klasse bezeichnet. Sie werden durch den Aufruf des Konstruktors initialisiert, d. h. benannt und im Rechner abgebildet. Erst die tatsächlich im Rechner abgebildeten Objekte besitzen konkrete Daten. Es können mehrere Objekte einer Klasse initialisiert werden.
Um unzulässige Zugriffe auf ein Objekt oder seine Variablen zu vermeiden, werden die Daten eines Objektes gekapselt. Durch die Kapselung wird der Zugriff auf die so genannten lokalen Variablen oder Membervariablen nur über definierte Schnittstellen zugelassen. Diese Schnittstellen sind meist Funktionen, denen bei ihrem Aufruf Parameter übergegeben werden. Das Objekt speichert diese übergebenen Daten, wenn nötig in lokalen Variablen. Danach führt es selbstständig die durch die Datenübergabe notwendigen Verarbeitungsschritte aus. Diese Vorgehensweise dient der Sicherheit der lokalen Daten und der Vermeidung versehentlicher Fehler. Auch die Abfrage der Membervariablen von außen erfolgt nach diesem Prinzip. Dabei wird die Funktion als Variable mit dem Datenformat des Rückgabewertes behandelt. Sie kann somit einer Variablen des gleichen Typs direkt zugewiesen werden.
Die Vererbung erlaubt es, eine neu zu entwickelnde Klasse von einer bereits vorhandenen Klasse (Oberklasse) abzuleiten. Dabei erbt die neue Klasse (Unterklasse) die Datenstruktur und die Funktionen der Oberklasse. Danach können weitere Parameter und Methoden hinzugefügt oder die geerbten Funktionen überschrieben werden. Durch die Vererbung ist es möglich, die Modellentwicklung hierarchisch aufzubauen. D. h., es wird eine Oberklasse mit den in allen Unterklassen notwendigen Parametern und Methoden entwickelt. Die Unter-klassen können dann wie ein Stammbaum mit einer "Ur-Klasse" aufgebaut werden. Somit ist es nicht mehr notwendig, in jeder Klasse die grundsätzlichen Daten und Funktionen neu zu definieren. Eine Klasse kann auch aus zwei oder mehr Vorgängern zusammengesetzt werden.
Die Funktionen eines Objektes können bei der objektorientierten Programmierung dynamisch festgelegt werden. Dabei ist der Aufruf einer Funktion mit ihrem Namen mehrdeutig. Das Objekt entscheidet anhand der Signatur des Aufrufs, welche Verarbeitungsweise ausgeführt werden soll. Die Signatur des Funktionsaufrufs besteht aus dem Format des Rückgabeparameters und aus der Reihenfolge bzw. dem Format der übergebenen Daten. Die Mehrdeutigkeit einer Funktion wird als Überladen bezeichnet. Mit dieser Vorgehensweise kann u. a. auch die Initialisierung eines Objektes durch das Überladen des Konstruktors dynamisch variiert werden.
Eine virtuelle Funktion wird verwendet, wenn in einer Oberklasse bereits eine Funktion festgelegt werden soll, die in allen Unterklassen mit derselben Signatur vorhanden ist. Dabei wird der entsprechende Programmablauf in jeder Unterklasse bestimmt. Die virtuelle Funktion kann dann mit dem Namen der Oberklasse aufgerufen werden. Es wird aber der Ablauf ausgeführt, der der Klasse des tatsächlich initialisierten Objektes entspricht. Wie bereits erwähnt, muss die Signatur in allen Klassen übereinstimmen. Wenn dies nicht der Fall ist, werden sie wie normale überladene Funktionen behandelt. Eine Klasse mit mindestens einer virtuellen Funktion ist eine virtuelle Klasse. Von einer virtuellen Klasse kann keine Instanz initialisiert werden.
Als erstes wird ein Hauptfenster als Objekt initialisiert, welches die Eingabe und Verarbeitung der vom Benutzer einzugebenden Daten sowie die Berechnung bzw. die Ausgabe des Lastgangs steuert. Zur Datenabfrage dienen Dialogfenster, die je nach gewünschter Eingabe (Lastgangdaten, Verbraucherdaten, usw.) aufgebaut werden. Diese Dialogfenster werden innerhalb eines Funktionsablaufs dynamisch erzeugt und kontrollieren die Eingaben selbst-ständig auf Fehler und Vollständigkeit. Nach der korrekten Eingabe erfolgt die Verarbeitung der Parameter in derselben Funktion. Die für die Simulation eines Lastgangs notwendigen Daten werden im Folgenden beschrieben.
Die Elektrogeräte, aus deren Energieverbrauch sich der Lastgang zusammensetzt, werden im Programmablauf dynamisch als Objekt initialisiert. Nach Kapitel 3.3 werden drei Klassen für die Darstellung der Verbraucher benötigt. Diese Verbraucherklassen werden von einer virtuellen Oberklasse abgeleitet und sind somit hierarchisch aufgebaut. Die "Ur-Klasse" heißt TVerbraucher, von der die Klassen der permanenten, der Ein-Aus und der Finite-State Verbraucher abgeleitet sind. Die für die Verbraucherklassen notwendigen Parameter und deren Methoden werden in den folgenden Abschnitten beschrieben. Die weiteren im Programm integrierten Möglichkeiten (z. B.: Verbraucherdatenbank, Lastgang drucken u. ä.) werden in dieser Arbeit nicht weiter behandelt.
Zu Begin einer Simulation werden die allgemeinen Daten des Lastgangs benötigt. Diese sind hier aufgelistet und ihre Eingabe und Verarbeitung wird an Hand eines Struktogramms (siehe Abbildung 4.1) erläutert.
 |
||
|
Mit diesen Angaben sind die charakteristischen Eigenschaften des Lastgangs festgelegt. Im Funktionsablauf werden sie nach der Eingabe initialisiert. Dabei setzt sich die Start- und Stoppzeit jeweils aus Datum und Uhrzeit zusammen. Wenn eine Stoppzeit - keine Dauer - eingegeben worden ist, muss die Dauer des Lastgangs berechnet werden. Die Schrittweite bestimmt die Abtastperiodendauer der Zeitdiskretisierung des zu simulierenden Lastgangs. Mit der Impulskonstante wird die Quantisierung der einzelnen zeitdiskreten Leistungswerte durchgeführt. Aus der Schrittweite und der Dauer wird vom Programm die Anzahl dieser Leistungswerte berechnet. Danach wird ein Feld mit der berechneten Anzahl an Gleitkommavariablen für die einzelnen Leistungswerte erstellt und im Speicher abgelegt. Ein Feld mit der gleichen Anzahl von Variablen wird benötigt, um die zufälligen Streuungen der Leistungswerte des Lastgangs festzulegen. Dies ist notwendig, weil diese Streuung für alle Verbraucher gleich sein soll. Mit der Streuung, die in % angegeben werden muss, wird dieses Feld mit zufälligen, nach der gaußschen Normalverteilung bestimmten Faktoren, gefüllt. Dieses Feld wird dem Verbraucher übergeben und dieser muss, soweit er der allgemeinen Streuung unterliegt, seine berechnete Last zum diskreten Zeitpunkt mit dem entsprechenden Faktor aus diesem Feld multiplizieren.
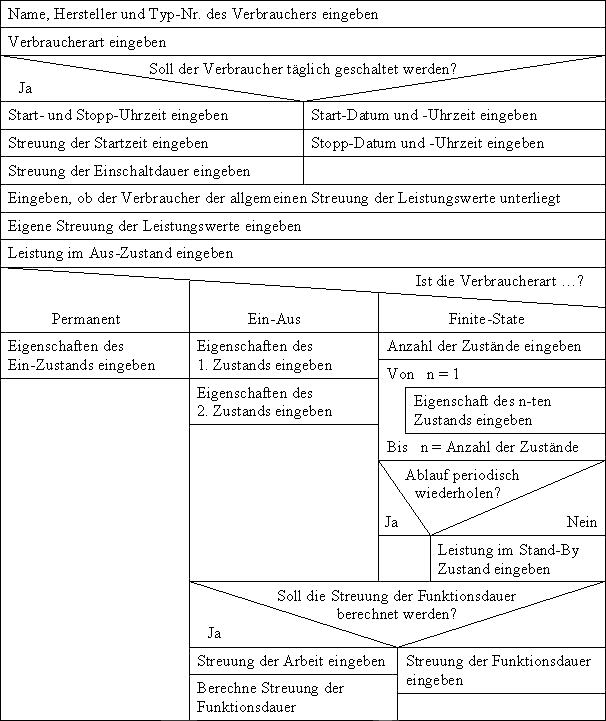
Um ein Verbraucher-Objekt initialisieren zu können, benötigt das Programm noch die charakteristischen Daten des Elektrogerätes, welches in den Lastgang einbezogen werden soll. Dazu gehören zunächst die Angaben, die für alle drei Verbraucherklassen gleich sind. Sie sind in der "Ur-Klasse" festgelegt.
|
||
|
Mit den im ersten Schritt eingegebenen Daten wird der Verbraucher eindeutig identifiziert. Das ist besonders im Hinblick auf die Verbraucherdatenbank wichtig. Die Art legt die Klasse fest, als dessen Instanz der Verbraucher initialisiert werden soll. Außerdem werden damit die objekttypischen Angaben, die noch benötigt werden, bestimmt. Die Schaltzeiten bestimmen die vier in Kapitel 3.3.1 beschriebenen Schaltmöglichkeiten aller Verbraucherklassen. Dabei muss als erstes definiert werden, ob der Verbraucher täglich mit den angegebenen Zeiten geschaltet werden soll oder nicht. Wenn nicht, dann muss nur die Start- und Stoppzeit mit Datum und Uhrzeit angegeben werden. Andernfalls wird die jeweilige Uhrzeit ohne Datum benötigt. Zusätzlich müssen dann die Streuungswerte der Startzeit und der Einschaltdauer bestimmt werden. Danach muss angegeben werden, ob der Verbraucher die in den allgemeinen Daten des Lastgangs definierte Streuung der Leistungswerte berücksichtigen soll. Es besteht auch die Möglichkeit, eine verbrauchereigene Streuung anzugeben. Als letztes wird die Leistungsaufnahme im ausgeschalteten Zustand, die nicht Null sein muss, benötigt.
Nun müssen noch die charakteristischen Parameter der gewählten Verbraucherklasse eingegeben werden. Die Klasse der permanenten Verbraucher benötigt nur noch die Angaben über die Eigenschaften des Ein-Zustands. Diese setzen sich bei dieser Klasse aus dem Verlauf, der Start-, der Endleistung und der Steigungsdauer zusammen. Der Verlauf kann dabei die in Kapitel 3.3.3 beschriebenen fünf Möglichkeiten annehmen.
Bei den Ein-Aus Verbrauchern müssen die Daten des 1. und 2. Zustands mit ihrem Verlauf, Start- und Endleistung, Steigungs- und Funktionsdauer und den Faktoren der ersten 3 Perioden angegeben werden. Zusätzlich wird noch die Streuung der Funktionsdauer benötigt. Diese kann direkt in Sekunden oder % eingegeben oder nach Vorgabe der Standardabweichung der Arbeit pro Tag oder pro Periode vom Programm berechnet werden.
Die Streuung der Funktionsdauer wird bei den Finite-State Verbrauchern gleichermaßen behandelt. Die Anzahl der Zustände (maximal 10 Zustände) und deren Eigenschaften sind wie zuvor bei den Ein-Aus Geräten anzugeben. Des Weiteren muss festgelegt werden, ob die Abfolge der Zustände periodisch wiederholt werden soll oder ob nach einem Durchlauf die Leistungsaufnahme bis zur Stoppzeit auf die dann vorzugebende Stand-By-Leistung gesetzt wird. Abbildung 4.2 zeigt das Struktogramm der Datenabfrage.
Im vorherigen Abschnitt, wurden die Parameter definiert, die ein Verbraucher-Objekt zur Simulation benötigt. Hier werden die Funktionen der Verbraucherklassen definiert. Eine Übersicht aller Funktionen zeigt die Tabelle 4.1. Sie zeigt auch, welche Funktionen in welcher Verbraucherklasse vorhanden sind. Virtuelle Funktionen der Klasse TVerbraucher sind mit einem V gekennzeichnet.

|
||
|
Übergebene Parameter: |
- Name des Verbrauchers (String),
- Hersteller des Verbrauchers (String), - Typ-Nr. des Verbrauchers (String), - Schrittweite der Abtastintervalle (Double), - Anzahl der zeitdiskreten Leistungswerte (Integer), - %-Wert der allgemeinen Streuung (Double), - Angabe, ob die allg. Streuung berücksichtigt wird (Bool). |
Durch den Aufruf des Konstruktors wird ein Verbraucher-Objekt initialisiert. Nach der Initialisierung wird das Objekt vom Hauptprogramm in eine Liste mit allen Verbrauchern eingetragen. Im Funktionsablauf des Konstruktors werden die übergebenen Daten in lokalen Variablen gespeichert. Für die zeitdiskreten Leistungswerte des Verbrauchers wird ein Feld mit der benötigten Anzahl von Double-Werten initialisiert.
Übergebene Parameter: |
- Startzeit des Lastgangs (Double),
- Schrittweite der Abtastintervalle (Double), - Anzahl der zeitdiskreten Leistungswerte (Integer), - %-Wert der allg. Streuung (Double). |
Diese Methode wird aufgerufen, wenn die Eigenschaften des Lastgangs geändert worden sind. Den Verbraucher-Objekten werden damit die neuen Daten übergeben. Im Funktionsablauf wird das alte Feld der Leistungswerte aus dem Speicher entfernt. Danach wird ein Feld mit der neuen Anzahl initialisiert. Nach dem Aufruf dieser Methode muss auch die Funktion "Berechne Leistungswerte" erneut durchgeführt werden.
Übergebene Parameter: |
- Startzeit des Lastgangs (Double),
- Startzeit des Verbrauchers (Double), - Stoppzeit des Verbrauchers (Double), - Angabe, ob der Verbraucher täglich geschaltet wird (Bool), - Streuung der Startzeit (Double), - Streuung der Einschaltdauer (Double). |
Die Methode "Setze Schaltzeiten" legt die übergebenen Parameter in lokalen Variablen ab.
Übergebene Parameter: |
- eigene Streuung der Leistungswerte (Double),
- Einheit der eigenen Streuung (Double), - Leistung im Aus-Zustand (Double), (permanenter Verbraucher) - Leistungsverlauf im Ein-Zustand (String), (Ein-Aus Verbraucher) - Leistungsverlauf im 1. Zustand (String), - Leistungsverlauf im 2. Zustand (String), - Streuung der Funktionsdauer (Double), - Einheit der Funktionsdauer-Streuung (String), (Finte-State Verbraucher) - Leistungsverläufe der Zustände (String), - Leistung im Stand-By Zustand (Double), - Streuung der Funktionsdauer (Double), - Einheit der Funktionsdauer-Streuung (String). |
Die in dieser Methode übergebenen Parameter sind für die Verbraucherklassen unterschiedlich. Sie werden im Funktionsablauf in Membervariablen gespeichert.
Übergebene Parameter: |
- Verlaufsform der Funktion (Integer),
- Startleistung der Funktion (Double), - Endleistung der Funktion (Double), - Steigungsdauer der Funktion (Double), - Startzeit der Funktion (Double), - Startzeit des zu berechnenden Integrals (Double), - Stoppzeit des zu berechnenden Integrals (Double). |
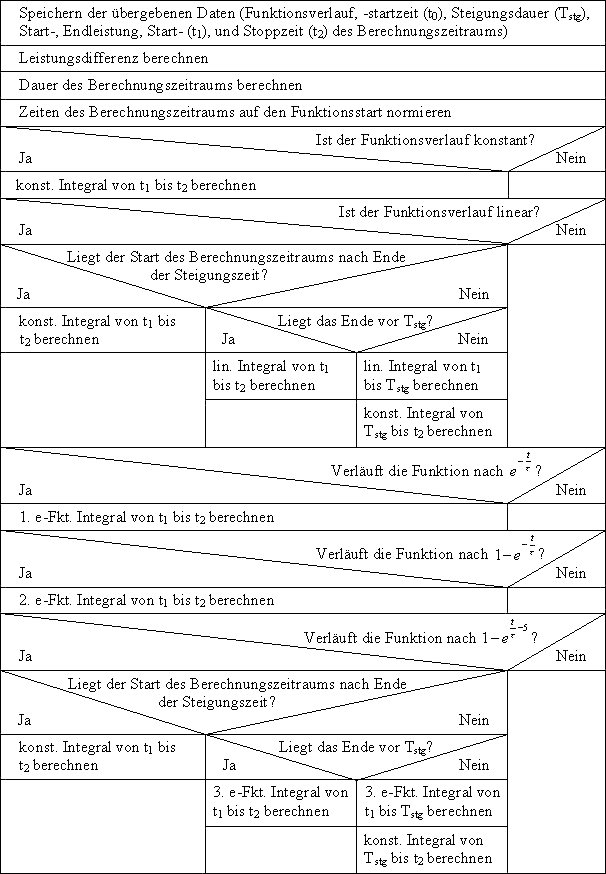
Die Funktion "Berechne mittlere Arbeit" ist in Abbildung 4.3 (Seite 43) dargestellt. Sie ist in allen Verbraucherklassen gleich. Ihr werden die Daten eines Funktionsverlaufs übergeben. Im Programmablauf wird das Integral dieser Funktion in den übergebenen Grenzen berechnet. Das Ergebnis dieser Berechnung wird als Double-Wert zurückgegeben.
Übergebene Parameter: |
- Faktoren der allgemeinen Streuung der Leistungswerte (Double-Feld),
|
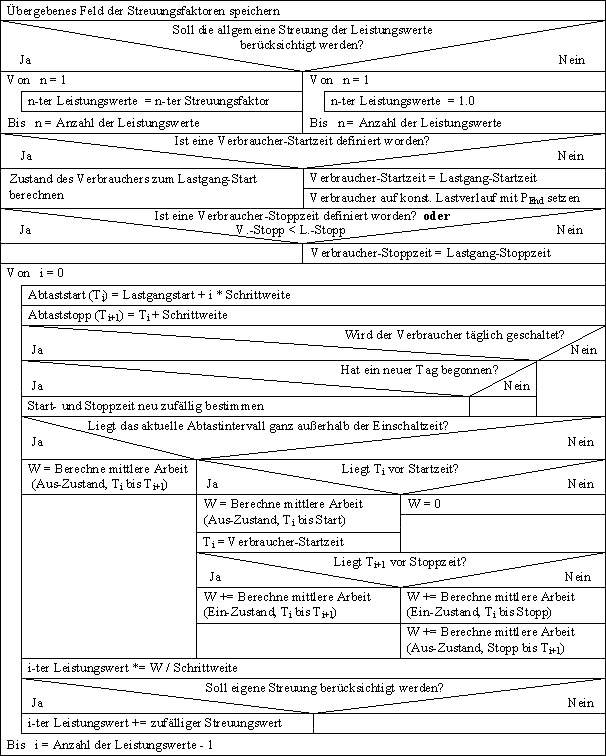
Diese Funktion berechnet die zeitdiskreten Leistungswerte der Verbraucher. Dazu wird das Feld mit den Faktoren (zufällig nach der gaußschen Normalverteilung bestimmt) der allge-meinen Streuung der Leistungswerte übergeben. Diese Methode ist abhängig von der Art des Verbrauchers und ist in den Abbildungen 4.4 bis 4.7 (Seite 44 - 47) für die verschiedenen Klassen dargestellt.
Übergebene Parameter: |
- Index des Leistungswertes (Integer),
|
Beim Aufruf der Funktion "Lese Leistungswert" wird der Index des gewünschten, zeitdiskreten Leistungswertes übergeben. Das Verbraucher-Objekt gibt dann den entsprechenden Wert im Double-Format zurück. Die Abfrage der einzelnen Leistungswerte dient dazu, sie von allen Verbraucher-Objekten in einer Schleife von 1 bis zur Anzahl der Leistungswerte abzurufen und zum resultierenden Lastwert zu addieren.
Die Methode "Lese Verbrauchereigenschaften" gibt die charakteristischen Eigenschaften des Verbraucher-Objektes in einer festgelegten String-Form zurück. Sie benötigt keine Parameterübergabe.
Die Methode "Lese berechnete Werte" dient dazu, bestimmte statistische Werte (z.B.: Energieverbrauch pro Tag oder während der Aus-Zustände) abzufragen. Die Werte werden bei der Berechnung der Leistungswerte bestimmt. Die Übergabe erfolgt auch mit Hilfe einer festgelegten String-Form. Die statistischen Werte können als Zusatzinformationen im Lastgang graphisch dargestellt werden. Die Berechnung dieser Werte ist in den Ablaufdiagrammen nicht berücksichtigt worden.
Diese Funktion ist nur in den Klassen der Ein-Aus und Finite-State Verbraucher vorhanden. Sie berechnet die prozentuale Streuung der Dauer der einzelnen Funktionsverläufe. Diese Berechnung erfolgt mit Gl. 3.15 - 17 & 3.19 - 20 (Seite 15 ff). Sie wird hier nicht näher erläutert.
Übergebene Parameter: |
- Verlaufsform der Funktion (Integer),
- Startleistung der Funktion (Double), |
Auch diese Methode ist nur in den Klassen der Ein-Aus und Finite-State Verbraucher vorhanden. Im Programmablauf wird mit den übergebenen Werten (mittleren Funktionsdauer und Streuung) die Zeit bis zum nächsten Zustandswechsel zufällig bestimmt und als Double-Wert zurückgegeben.
Der Destruktor wird aufgerufen, um ein nicht mehr benötigtes Objekt aus dem Speicher zu entfernen. Er sorgt dafür, dass der Speicherbereich aller im Konstruktor initialisierten lokalen Variablen wieder freigegeben wird.
In Abbildung 4.3 ist die Methode "Berechne mittlere Arbeit", die bei allen Verbraucherarten gleich ist, dargestellt. Es wird gezeigt, wie das Integral, mit den an die Methode übergebenen Zeiten, je nach Verlaufsform der Funktion bestimmt wird. Dabei werden die Formeln zur Berechnung aus Kapitel 3.4 nicht gesondert aufgeführt.
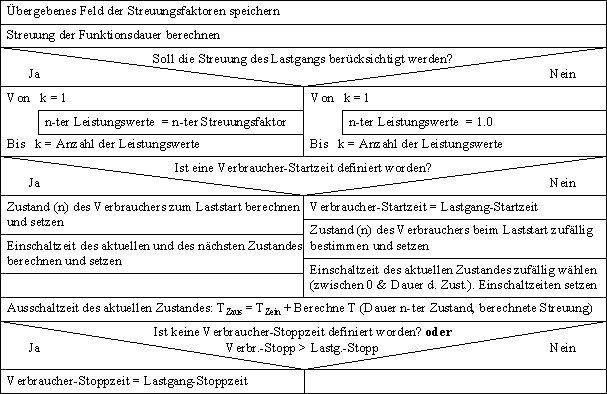
Die Berechnung der zeitdiskreten Leistungswerte bei einem permanenten Verbraucher zeigt die Abbildung 4.4 (Seite 44). Die Eingabe des Feldes der Streuungsfaktoren erfolgt - wie bereits erwähnt - mit dem Aufruf dieser Methode. Ob diese Faktoren berücksichtigt werden, wird danach entschieden. Wenn keine Verbraucher-Startzeit eingegeben wurde oder die eingegebene kleiner als die Startzeit des Lastgangs ist, wird sie gleich der Lastgang-Startzeit gesetzt. Da in diesem Fall der Verbraucher auch vor dem betrachteten Zeitraum bereits eingeschaltet war, darf sein Leistungsverhalten beim Start nicht berücksichtigt werden. Dazu wird er, wenn er keinen konstanten Lastverlauf besitzt, auf einen solchen mit der Endleistung gesetzt. Im Anschluss wird mit einer for-Schleife jeder einzelne Leistungswert berechnet. Es wird dabei zuerst die Start-
Bei den Ein-Aus und Finite-State Verbrauchern ist der Ablauf ähnlich. Der erste Teil ist bei beiden Arten gleich (Abbildung 4.5 / Seite 45). Dabei wird zusätzlich zum permanenten Verbraucher die prozentuale Streuung der Funktionsdauer berechnet. Der Zustand beim Start des Lastgangs wird zufällig gewählt bzw. berechnet, wenn keine Verbraucher-Startzeit vorgegeben wurde oder diese kleiner als der Lastgangstart ist. Die Start-
|
||
|
|
||
|
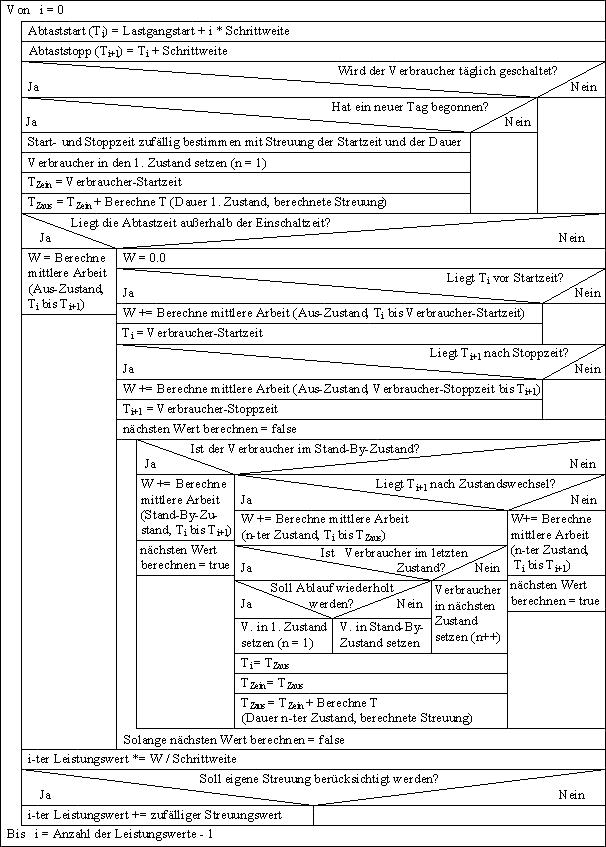
Die Abbildung 4.6 (Seite 46) zeigt die Fortsetzung der Methode "Berechne Leistungswert" der Ein-Aus Verbraucher. Auch bei dieser Verbraucherart wird jeder einzelne zeitdiskrete Leistungswert in einer for-Schleife berechnet. Dazu wird wiederum der Abtastzeitraum mit Start-
|
||
|

|
||
|
|
||
|